MOTORS
(AKA MOMENT-VECTORS AKA MOTION VECTORS AKA SCREWS SEE ALSO DUAL QUATERNIONS AKA BIQUATERNIONS )
WHAT DO THEY DO?
1. A MOTOR in 2D or 3D COMBINES DISPLACEMENT AND ROTATION into ONE MULTIPLICATION.
2. THEY ARE USED IN, AMONGST OTHER THINGS, CRAZY PHYSICS
SUPERSPACES (WHAT ISN'T?). Er, the Primary part of a Dual Number is a
Boson (a Force) and the Secondary a Fermion (oh, you know, matter, leptons quarks, etc).
In otherwords (and other worlds), Dual Multivectors can be used to describe a particle-wave Duality!
3. AWESOME! Do I Know how to do that? Not a chance!
4. DUAL QUATERNIONS are used a lot in RIGID BODY MECHANICS (i.e. ROBOT ARMS)
and LINKAGES. ALSO, it has uses in THE FALLING CAT PROBLEM, heat AND energy
AND light transfer, flux, WHAT HAVE-YOU. If you look up PLÜCKER SPACE you'll
find references for RAY TRACING SOLUTIONS (using the MOTOR (i.e. CROSS) PRODUCT between two oriented lines
in spatial geometry).
5. ARRGH! ENOUGH NONSENSE. What Do I need to Know?
INTRO:
DUAL NUMBERS, VECTORS, and QUATERNIONS can be written with this (^) circumflex above them.
Since it is easier to insert a Circumflex about a vowel in html we'll call our DUAL VECTOR Â
They can be ALSO written like Complex pairs are: 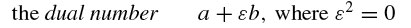 Sometimes the circumflex might be seen above a theta (A DUAL ANGLE), which means the theta has a distance AND an slide or screw attached to it (a variable s):
Sometimes the circumflex might be seen above a theta (A DUAL ANGLE), which means the theta has a distance AND an slide or screw attached to it (a variable s):
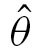 is the same as
is the same as 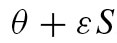 (an angle θ and a displacement S).
(an angle θ and a displacement S).
That's hard to write up in mark-up too, let's call it Ô here.
TWELVE STEPS TOWARDS SCREW-DOM
Step 1: Think about the most basic DUALITY: two points define a line, and two lines define a point.
Step 2: Remember whatever you know off-the-cuff about Quaternions. Remember, for instance, that a "pure" Quaternion, with a Zero Scalar value, is a 3D vector projected into a higher dimensional representation. (i.e. V(x, y, z) : Q(0, x, y, z) ). Remember that you can rotate a Vector V onto V' by a Quaternion Q such that V' = Q V Q* (where Q* is the conjugate of Q and V undergoes conversion into the Pure Quaternion representation of it). If we know the axis A and angle θ we want to rotate the vector, we can derive Q from it (Cos θ/2 + A Sin θ/2). This representation is a "Spinor" (I think).
Step 3: Forgive my atrocious mathematical notation. I know nothing about proper etiquette here.
Step 4: Hmm, I don't remember.
Step 5: Take a Look at this chart I stole from this excellent paper about Clifford and his Algebra:
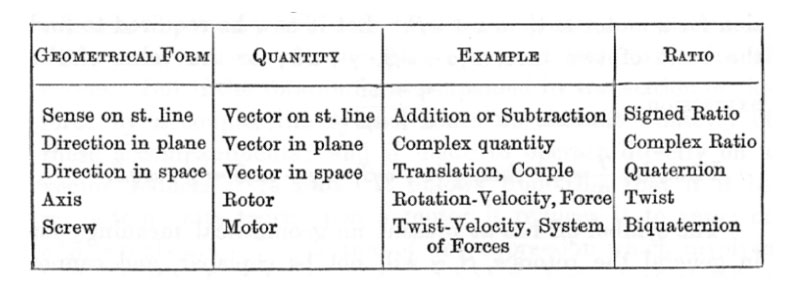
Rooney, p95: Table 1. Summary of geometrical forms and their representations.
(W.K. Clifford, 1882, Collected Papers, p. 188, Chelsea Publishing Company, New York)
Step 6: From the chart we see it is now time to accept something terrible: Quaternions and Vectors aren't enough! They are very useful when we are dealing with a spherical geometry, where all lines intersect at the origin, and we want to swivel about in spherical coordinates, or spin and spin and spin. BUT we also want to slide and scuttle and shuffle and twist. This is what DUAL numbers are useful for: Spatial Geometry. Instead of reflecting us about this and that (er, X and Y), they twist and scoot us about this and that.
Step 7: What is a Dual Vector then? Let's see, it sounds like it means there are two vectors combined into one, is that true? Well, pretty much! A Dual Vector is two points that define a line, but not the typical way. Instead of drawing a line between point P and point P', we use point P to define the direction of the line and point P' to define its moment about the origin (specifically, this second point, the "moment", is the cross product between point A and any point on the line, though usually just the point closest to the origin). Specifically, any oriented line in space can be defined by its 6 Plücker Coordinates (l, m, n, l0, m0, n0) where l, m, and n are the direction of the line and l0, m0, and n0 are the moment.
Step 8: Ah, I remember Step 4 now! Remember the complex numbers (a + bi) are useful for reflecting about axes when you multiply them together because i2 = -1. A DUAL number is LIKE a complex number except the imaginary i is written as ε (epsilon) and so we write (a + bε), and get ready? ε 2 = 0. Huh? Well, that nifty habit of squaring to zero allows us use the "imaginary" part to shift and slide rather than reflect. We don't really call it "real" and "imaginary" in Dual numbers as much as "primary" and "secondary" (or, er, in particle physics, bosonic and fermionic elements). So What? Well, Plücker coordinates can also be written as a vector of dual numbers l + εl0, m + εm0, n + εn0) -- in other words, as a Dual Vector (or a vector of dual numbers -- it's the same thing).
Step 9: Just like a regular Vector can be represented by a Pure Quaternion, so can Dual Vectors be represented by a Dual Quaternion (also known as a Unit Dual Quaternion). A Dual Quaternion Q^ can be defined as two Quaternions: Q^ = Q + εQ. For notation purposes let's write Î = Q + εQ. Just like in Dual Numbers, there is a Primary part and a Secondary part. To represent a Dual Vector as a Dual Quaternion, you do what you would normally do to represent a regular vector as a regular quaternion (if you normally do this sort of thing). Remember a Plücker Coordinate is a Dual Vector.
Step 10. To represent a screw-like motion, you need a skew axis, an angle of rotation about that axis, and a distance moved along it as well. The Plucker Coordinate or Dual Vector, is our Skew Axis. A Dual Angle represents our rotation about the axis and movement along it. Just as we derived a Quaternion Q to "rotate" Vector V onto V', we can derive a Dual Quaternion Î to "screw" Dual Vector  onto Â'. It is similar too. Given a Plucker ( Dual Vector ) Skew Axis  and a Dual Angle Ô we can define a Dual Quaternion Î = Cos Ô/2 + Sin Ô/2 * Â.
Step 11. Extending this out amounts to an equation that I am going to copy and paste here (Rooney writes n^ instead of Â, and basically derives it by expanding the identity defining how to take the cos and sin of a dual angle, which is not hard ).
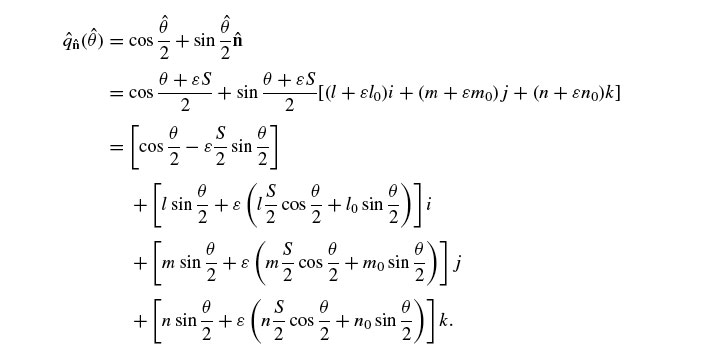 Step 12. Learn More! Read this excellent and clearly written paper on William Clifford and Biquaternions by Joe Rooney. Books: Geometric Design of Linkages, and Geometric Basics of Robotics.
Flipcode has a strange tutorial on Plücker Coordinates
Step 12. Learn More! Read this excellent and clearly written paper on William Clifford and Biquaternions by Joe Rooney. Books: Geometric Design of Linkages, and Geometric Basics of Robotics.
Flipcode has a strange tutorial on Plücker Coordinates
Next to Read: "Octonions, a Development of Clifford's Biquaternions" by Alexander McAulay. And Description of the conformations of complex molecules by means of dual quaternions, etc . . .
Other Fun Facts:
The motor, or cross, product of two dual quaternions (or two dual vectors) returns a scalar that who's sign defines the side to which one line passes the other. If the scalar is zero, the lines are parallel or they intersect.
Conjugation can be used to extract the scalar and vector parts of a quaternion. The scalar part of p is (p + p*)/2, and the vector part of p is (p − p*)/2. The X of two quaternions returns the cross of their vector part.
In a Dual Vector representation of a line, the cross product of the primary and secondary part is a point on the line passes.
Since Dual Vectors Define an Oriented Line, Two of them should represent a single point (if they intersect). How can we quickly test to see if Dual Vectors Intersect? Well, we can test to see if they are parallel.
Given a Rotation (axis, angle) and Translation Vector t, what is the Dual Quaternion Representation?
q = from(R); q' = .5*(q(t))
HERE's a RECAP
THE SET OF ORIENTED LINES IN SPACE
DUAL QUAT: qˆ = q + εq' = a0 + a1i + a2j + a3k + ε(a' 0 + a'1 i + a'2 j + a'3 k).
PLUCKER: P = (l, m) 0 lx ly lz 0 mx my mz
(Corresponds to Unit Dual Vector Quaternions)
The Transfer Principle (Geometric Facts in Point Geometry become Geometric Facts in Line Geometry with Duals)
Question: Given Two Lines (la, ma) and (lb, mb) what is the Dual Quaternion that describes the operation.
From Rooney:
The relative spatial relationship of two general dual vectors Aˆ and Bˆ requires
eight parameters for its specification. Four of these define the common
perpendicular line between the axes of the motors; two more specify the dual
angle between these axes; and finally two parameters are required to represent
the ratios of the two magnitudes associated with the second motor to those
associated with the first.

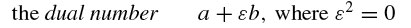 Sometimes the circumflex might be seen above a theta (A DUAL ANGLE), which means the theta has a distance AND an slide or screw attached to it (a variable s):
Sometimes the circumflex might be seen above a theta (A DUAL ANGLE), which means the theta has a distance AND an slide or screw attached to it (a variable s): 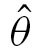 is the same as
is the same as 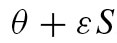 (an angle θ and a displacement S).
(an angle θ and a displacement S).

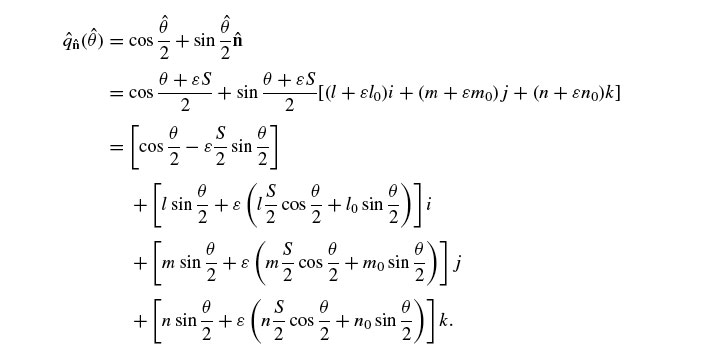 Step 12. Learn More! Read this excellent and clearly written paper on William Clifford and Biquaternions by Joe Rooney. Books: Geometric Design of Linkages, and Geometric Basics of Robotics.
Flipcode has a strange tutorial on Plücker Coordinates
Step 12. Learn More! Read this excellent and clearly written paper on William Clifford and Biquaternions by Joe Rooney. Books: Geometric Design of Linkages, and Geometric Basics of Robotics.
Flipcode has a strange tutorial on Plücker Coordinates